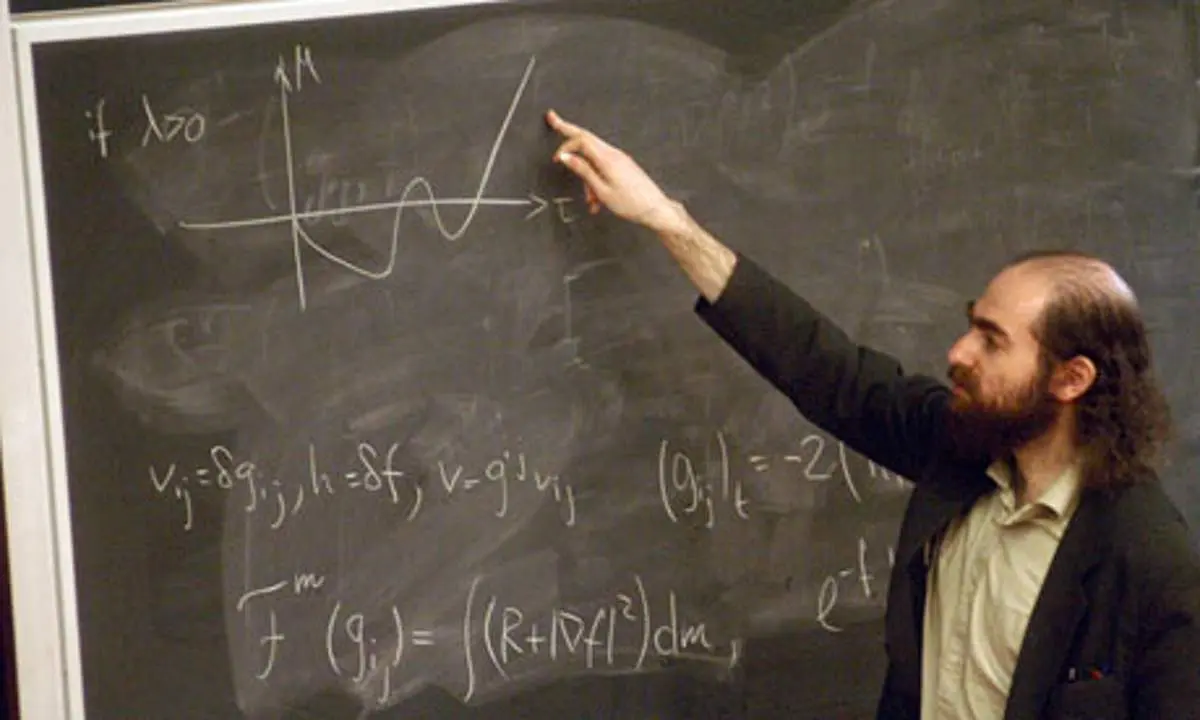โจทย์คณิตศาสตร์ที่ยากที่สุด ที่มนุษย์ยังไม่สามารถหาคำตอบได้

Millennium Prize Problems
หรือ 'ปัญหารางวัลมิลเลนเนียม'
คือชุดของปัญหาทางคณิตศาสตร์ จำนวน 7 ข้อ ที่ยังไขไม่ได้
ซึ่งระบุโดยสถาบันคณิตศาสตร์เคลย์ ในปี 2543 สถาบันประกาศว่า
ใครก็ตามที่แก้ปัญหาเหล่านี้ได้สำเร็จ (เพียงหนึ่งใน 7 ข้อ)
จะได้รับรางวัลเป็นจำนวนเงินหนึ่งล้านดอลลาร์
(ประมาณ 34 ล้านบาท) ปัญหาครอบคลุมด้านต่างๆ ของคณิตศาสตร์
และถือเป็นปัญหาที่ท้าทายและสำคัญที่สุดในสาขานี้
นี่คือคำอธิบายสั้นๆ ของแต่ละปัญหา (ปัญหาในทางคณิตศาสตร์)

 
การคาดคะเนของ Birch และ Swinnerton-Dyer
(Birch and Swinnerton-Dyer conjecture)
ปัญหานี้เกี่ยวข้องกับเส้นโค้งวงรี ซึ่งเป็นวัตถุทางคณิตศาสตร์ประเภทหนึ่ง
และความเชื่อมโยงกับทฤษฎีจำนวน มันเสนอว่ามีความสัมพันธ์พื้นฐาน
ระหว่างจำนวนจุดตรรกยะบนเส้นโค้งวงรี และคุณสมบัติบางอย่าง
ของฟังก์ชันทางคณิตศาสตร์ที่เกี่ยวข้องกันของเส้นโค้ง

ข้อความคาดการณ์ของฮอดจ์
(Hodge Conjecture)
ปัญหาเกี่ยวข้องกับวัฏจักรเกี่ยวกับพีชคณิต ซึ่งเป็นวัตถุทางเรขาคณิต
ที่กำหนดไว้ในเรขาคณิตเกี่ยวกับพีชคณิต การคาดเดาชี้ให้เห็นว่าวัฏจักรบางประเภท
สามารถแสดงเป็นการรวมกันของวัฏจักรที่ง่ายกว่าได้

ปัญหาการมีอยู่ของนาเวียร์-สโตกส์และความราบเรียบ
(Navier–Stokes existence and smoothness)
ปัญหานี้เกี่ยวข้องกับการเปลี่ยนแปลงของของไหล และพฤติกรรมของการไหลของของไหล
มันพยายามที่จะพิสูจน์ว่าคำตอบของสมการ Navier-Stokes
ซึ่งอธิบายการเคลื่อนที่ของของไหลนั้นมีอยู่จริง และยังคงราบรื่นตลอดเวลาหรือไม่

ปัญหาพีและเอ็นพี
(P versus NP problem)
ปัญหานี้อยู่ในขอบเขตของทฤษฎีความซับซ้อนทางการคำนวณ
ถามว่าทุกปัญหาที่โซลูชันสามารถตรวจสอบได้อย่างมีประสิทธิภาพ
สามารถแก้ไขได้อย่างมีประสิทธิภาพหรือไม่

สมมติฐานรีมันน์
(Riemann hypothesis)
เสนอโดยแบร์นฮาร์ด รีมันน์ ปัญหานี้เกี่ยวข้องกับการกระจายของจำนวนเฉพาะ
มันเกี่ยวข้องกับตำแหน่งของศูนย์ที่ไม่สำคัญของฟังก์ชันซีตาของ Riemann
และแนะนำว่าพวกมันทั้งหมดอยู่บนเส้นเฉพาะในระนาบเชิงซ้อน

ปัญหาการมีอยู่ของทฤษฎีหยาง-มิลส์ และมวลพื้น
(Yang–Mills existence and mass gap)
ปัญหานี้เกี่ยวข้องกับทฤษฎีสนามควอนตัม มีจุดมุ่งหมายเพื่อตรวจสอบว่า
ทฤษฎี Yang-Mills ซึ่งอธิบายพฤติกรรมของอนุภาคมูลฐานมีช่องว่างมวลหรือไม่
(หมายถึงมีความแตกต่างของพลังงานระหว่างสถานะพื้นและสถานะตื่นเต้นต่ำสุด)

ข้อความคาดการณ์ของปวงกาเร
(Poincaré conjecture)
ปัญหานี้เสนอโดย Henri Poincaré เดิมทีเกี่ยวข้องกับรูปร่าง
และโทโพโลยีของปริภูมิสามมิติ
มันถามว่าทุกๆสามมิติที่เชื่อมต่อกันง่ายๆ สามมิติแบบปิดนั้น
เป็นโฮมีโอมอร์ฟิคเป็นสามมิติหรือไม่ (วัตถุทางเรขาคณิตประเภทหนึ่ง)

(Grigori Perelman
คนแรกที่พิสูจน์ 1 ใน 7 ปัญหานี้ได้สำเร็จ)

ปัญหาเหล่านี้ได้รับการพิสูจน์แล้วว่ายากเป็นพิเศษ
และจนถึงตอนนี้ มีเพียงข้อเดียวในนั้น นั่นคือ
'ข้อความคาดการณ์ของปวงกาเร' (Poincaré Conjecture)
ที่ได้รับการพิสูจน์จนสำเร็จ โดย Grigori Perelman นักคณิตศาสตร์ชาวรัสเซีย
ซึ่งได้พิสูจน์สำเร็จในปี 2546 อย่างไรก็ตาม เขาปฏิเสธเงินรางวัลจำนวนนี้